Toán 11 - Ôn tập đầu năm

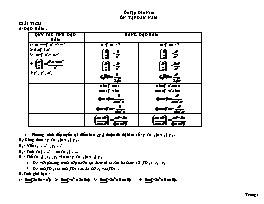
ÔN TẬP ĐẦU NĂM
GIẢI TÍCH 
A/ ĐẠO HÀM .
QUY TẮC TÍNH ĐẠO HÀM
BẢNG ĐẠO HÀM
1/ (u+v-w)’=u’+v’-w’ 
2/ (k.u)’=k.u’ 
3/ (uv)’=u’.v+u.v’ 
4/ 
5/ y’x=y’u.u’x
(xn)’=nxn-1
=
=
(un)’=nun-1
=
=
(sinx)’=cosx
(cosx)’=-sinx
(sinu)’=u’.cosu
(cosu)’=-u’.sinu
 Phương trình tiếp tuyến tại điểm M(x0;y0) thuộc đồ thị hàm số : y=f’(x0)(x-x0)+y0 .
B1: Công thức : y=f’(x0)(x-x0)+y0 .
B2 : Viết x0=.? , y0=? 
B3 : Tính f’(x)=.? f’(x0)=..
B4 : Thế f’(x0) , x0 , y0 vào ct : y=f’(x0)(x-x0)+y0
Để viết phương trình tiếp tuyến tại điểm M ta cần ba tham số : f’(x0) , x0 , y0 .
Để tính f’(x0) ta tính f’(x) sau đó thế x0 vào f’(x) .
B. Tính giới hạn : 
1/ 	2/ 	 3/ 	4/ .
5/ 	 6/ 7/ 8/ 
9/ 	10/ 11/ 	12/ 13/ 14/ .
C. Tính giá trị của hàm số :
	Bài 1: Cho hàm số y= .Tính f(0) , f(1), f(-1), f(2),f(-2) ,f(3),f(-3) ,f() , f(-) .
	Bài 2: Cho hàm số y= .Tính f(0),f(1),f(-1),f(2),f(-2),f(),f(-),f() .
D. Biểu diễn các điểm sau trên hệ trục tọa độ Oxy : A(2;1),B(-3;2),C(-4;-1),D(0;-4),E(3;0),F(-2;0) G(0;2)
E. Vẽ các đường thẳng sau trên hệ trục tọa độ Oxy : y=1 , y=2,y=-3 ,y=x , x=-2,x=3 , y=2x-2 , y=-3x+1 .
F / GIẢI PHƯƠNG TRÌNH 
I/ Phương trình bật nhất : ax+b=0 (a) Cách giải : .
II/ Phương trình bậc hai : 
Trường hợp 1: Pt đầy đủ hệ số a,b,c .Ta giải bằng cách tính hoặc .
 với b’= .
< 0 : Pt vô nghiệm .
= 0 : Pt có nghiệm kép 
> 0 : Pt có 2 n0 phân biệt :
<0 : Pt vô nghiệm .
= 0 : Pt có nghiệm kép 
> 0 : Pt có 2 n0 phân biệt :
Bài tập áp dụng : Giải các phương trình sau bằng cách tính hoặc .
1/ 	2/ 
3/ 	4/ 	
 5/ . 6/ 
 7/ 	8/ 	
 9/ 
 Trường hợp 2: Pt khuyết c , tức là c=0 . 
 Cách giải : Đặt thừa số chung đưa về pt tích :
Bài tập áp dụng : Giải các pt sau bằng cách đặt thừa số chung :
1/ 	2/ 	3/ 	4/ 	5/ 
Trường hợp 3: Pt khuyết b , tức là b=0 . Giải bằng cách chuyển vế lấy căn bậc hai 2 vế
Cách giải : . Chú ý : .
Bài tập áp dụng : Giải các pt sau bằng cách chuyển về và lấy căn hai vế :
1/ 	 2/ 	 3/ 	4/ 	5/ .
Trường hợp 4 : Pt khuyết b,c , tức là b=0 , c=0 . (chú ý : a)
VD : 	2/ 	3/ 	4/ 
G/ XÉT DẤU NHỊ THỨC BẬC NHẤT f(x)=ax+b (a) .
	B1: Tìm nghiệm x=
x
- +
f(x)
 Trái dấu a 0 Cùng dấu a 
B2: Lập bảng xét dấu : 
Bài tập: Xét dấu các nhị thức sau : 1/ f(x)=2x-2	2/ f(x)=-3x-1 3/ f(x)=-2x 
H/ XÉT DẤU TAM THỨC BẬC HAI : f(x)= (a) .
	1/ Trường hợp 1: f(x) vô nghiệm f(x) cùng dấu với a .
x
- +
f(x)
 Cùng dấu a 
Lập bảng xét dấu : 
2/ Trường hợp 2: f(x) có nghiệm kép f(x) cùng dấu với a 
(Chú ý: Tại x= f(x) bằng 0 )
x
- +
f(x)
 Cùng dấu a 0 Cùng dấu a
 Bảng xét dấu :
3/ Trường hợp 2: f(x) có 2 nghiệm phân biệt . Xét dấu trong trái ngoài cùng .
 Bảng xét dấu :
x
- x1 x2 +
f(x)
 Cùng dấu a 0 Trái dấu a 0 Cùng dấu a
Bài tập : Xét dấu các tam thức bậc hai sau : 1/ f(x)=	2/ f(x)=
3/ f(x)=	4/ f(x)=	5/ f(x)=	6/ f(x)=	7/ 
8/ f(x)=	9/ f(x)=	10/ f(x)= với m>0 . 11/ f(x)= , a<0 .
I/ Giải phương trình bậc ba : 
	1/ Cách 1: Sử dụng máy tính .
	2/ Nhẩm nghiệm rồi chia đa thức đưa về pt bậc nhất và bậc hai .
Bài tập : Giải các phương trình sau : 1/ 2/ 3/ 
4/ 	5/ 	6/ 	7/ 
J/ Xét dấu đa thức bậc ba : f(x)=
Tìm nghiệm .
Lập bảng xét dấu : Khoảng đầu tiên trái dấu với a , qua đơn kép đổi dấu , qua nghiệm kép không đổi dấu .
Bài tập : Xét dấu các đa thức : 1/ f(x)=	2/ f(x)=	3/ f(x)=
4/ f(x)=	5/ f(x)=	6/ f(x)=	7/ 	8/ 
LÝ THUYẾT VÀ BÀI TẬP HÌNH HỌC ÔN TẬP ĐẦU NĂM 
1/ TAM GIÁC :
Diện tích S= . S= . S= 
Diện tích S= (p=) . 
Diện tích S=
Chú ý : Tính diện tích và tính chiều cao của tam giác . 
 và .
Diện tích : S= . S= .
Định lý pitago : hay 
(Bình phương cạnh huyền bằng tổng bình phương 2 cạnh góc vuông ) .
 suy ra : .
ah.=bc , , 
Tỉ số lượng giác :
Tìm sin lấy đối chia huyền 
 , , tanB= , cotB= 
	Gọi I là trung điểm của BC :
AI là đường trung tuyến .
IA=IB=IC (trung tuyến ứng với cạnh huyền bằng một phận hai cạnh huyền) . I là tâm của đường tròn ngoại tiếp tam giác ABC . Người ta còn gọi I là tâm của tam giác vuông .
3/ TAM GIÁC CÂN :
AB=AC .
Gọi M là trung điểm BC , AM là đường trung tuyến và cũng là 
đường cao , trung trực , phân giác .
 3. .Diện tích S= .
TAM GIÁC ĐỀU .
AB=AC=BC=a .
Gọi H là trung điểm BC , khi đó AH là đường trung tuyến và cũng là 
đường cao , trung trực , phân giác .
 3. . AH= (đường cao = độ dài cạnh nhân chia cho 2 )
 4. Diện tích S= , S=
HÌNH BÌNH HÀNH :
AB//DC và AB=DC , AD//BC và AD=BC .
Hai đường chéo AC và BD cắt nhau tại trung điểm mỗi đường .
AH=h là đường cao .Khi đó AHDC và diện tích S=2..
HÌNH THANG CÂN :
AB//DC , AB=b đáy nhỏ , DC=a đáy lớn . 
AD và BC cạnh bên . AD=BC .
Hai đường chéo AC và BD : AC = BD , AC cắt BD tại trung điểm mổi đường . 
AH là đường cao . Khi đó : AHDC . Diện tích S=.
HÌNH CHỮ NHẬT :
AB=DC=a , AD=BC =b . Góc : . 
BC , AD DC , DC BC 
2 đường chéo = nhau , cắt nhau tại trung điểm O của mỗi đường . 
OA=OB=OC=OD . 2 đường chéo không vuông góc với nhau .
O là tâm hình chữ nhật . Hay O là tâm đường tròn ngoại tiếp 
Hình chữ nhật . Người ta gọi hình chữ nhật nội tiếp đường tròn .
Diện tích : S=a.b .
HÌNH VUÔNG :
AB=BC=CD=DA=a . Góc : . 
BC , AD DC , DC BC 
2 đường chéo = nhau , cắt nhau tại trung điểm O của mỗi đường .
OA=OB=OC=OD . 2 đường chéo vuông góc với nhau . ACBD .
O là tâm hình vuông , hay Olà tâm đường tròn ngoại tiếp hình vuông .
Diện tích : S=a.a=a2
 10 .HÌNH THOI :
AB=BC=CD=DA . AC BD . BD không bằng AC .
Hai đường chéo cắt nhau tại trung điểm mỗi đường : OA=OC , OB=OD .
Diện tích S= .
 HÌNH HỌC KHÔNG GIAN .
1/ Các hình biểu diễn cửa hình tứ diện ABCD .
2/ Các hình biểu diễn của hình chóp tứ giác 	S.ABCD .
3/ Định nghĩa hình chóp đều : Một hình chóp gọi là hình chóp đều , nếu đáy của nó là đa giác đều và các cạnh bên bằng nhau . 
Một hình chóp là hình chóp đều đáy của nó là đa giác đều và đường cao của nó đi qua tâm của đáy (tâm của đáy chính là tâm của tròn tròn ngoại tiếp đa giác đáy).
Một hình chóp là hình chóp đều đáy của nó là đa giác đều và các cạnh bên tạo với mặt đáy các góc bằng nhau .
Các cạnh bên của hình chóp đều bằng nhau . Các mặt bên là các tam giác cân .
Chú ý : 
Tam giác đều có tâm là giao điểm hai đường trung tuyến . 
Tam giác vuông có tâm là trung điểm cạch huyền . 
Tam giác thường , tam giác cân có tâm là giao điểm hai đường trung trực .
Hình chữ nhật , hình vuông , hình thoi có tâm là giao điểm hai đường chéo
3.1 Hình chóp tam giác đều : S.ABC . 
 AB=BC=AC . SA=SB=SC . AH là đường cao : .
H là tâm của đường tròn ngoại tiếp tam giác đều ABC .
H là giao điểm của của hai đường trung tuyến .
 , . HA=HB=HC .
Góc của cạnh bên SA và mặt đáy (ABC) chính là góc của SA 
và hình chiếu của SA lên mp(ABC) là AH hay AM .
Vậy : hay.
Thể tích khối chóp : S= 
 3.2 . Cách vẽ hình chóp tam giác đều :S.ABC .
Bước 1: Vẽ mặt đáy là tam giác đều ABC .
Bước 2: Xác định tâm H của đều ABC ,(H là giao điểm của 2 đường trung tuyến AM và BN)
Bước 3: Dựng đường thẳng qua tâm H và vuông góc mặt đáy .
Bước 4: Trên lấy điểm S (khác H) . Nối SA,SB,SC ta được hình chóp tam giác đều 
 3.3 Cách vẽ hình tứ diện đều ABCD . 
Bước 1: Vẽ mặt đáy là tam giác đều BCD .
Bước 2: Xác định tâm H của đều BCD ,(H là giao điểm của 2 đường trung tuyến BM và CN)
Bước 3: Dựng đường thẳng qua tâm H và vuông góc mặt đáy .
Bước 4: Trên lấy điểm A (khác H) . Nối AB,AC,AD ta được hình tứ diện đều .
Chú ý : Ta có thể chọn tam giác ACB hoặc ACD hoặc ABD làm mặt đáy .
 3.4 . Cách vẽ hình chóp tứ giác đều : S.ABCD .
Bước 1: Vẽ mặt đáy là tứ giác đều ABCD .
Bước 2: Xác định tâm H của tứ giác đều ABCD ,(H là giao điểm của 2 đường chéo AC và BD .
Bước 3: Dựng đường thẳng qua tâm H và vuông góc mặt đáy .
Bước 4: Trên lấy điểm S (khác H) . Nối SA,SB,SC, SD ta được hình chóp tứ giác đều
GHI CHÚ : Hình tứ diện đều là hình có tất cả các cạnh bằng nhau , tất cả các mặt là các tam giác đều
Đa giác đều n đỉnh
Giả sử đa giác A1A2A3An có cạnh bằng a , có diện tích là S ta có S =