Kiến thức cơ bản phương trình lượng giác

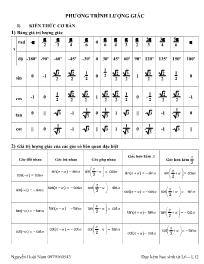
Nguyễn Hoài Nam 0979160543 Dạy kèm học sinh từ L6 – L12 
PHƯƠNG TRÌNH LƯỢNG GIÁC 
I) KIẾN THỨC CƠ BẢN 
1) Bảng giá trị lượng giác 
x 
rad - -

2
 -

3
 -

4
 -

6
 0 

6

4

3

2
2
3
3
4
5
6
  
độ -180o -90o -60o -45o -30o 0 30o 45o 60o 90o 120o 135o 150o 180o 
sin 0 -1 -
3 
2
 -
2 
2
 -
1
2
 0 
1
2
2 
2
3 
2
 1 
3 
2
2 
2
1
2
 0 
cos -1 0 
1
2
2 
2
3 
2
 1 
3 
2
2 
2
1
2
 0 - 
1
2
 -
2 
2
 -
3 
2
 -1 
tan 0 || - 3 -1 -
1
3 
 0 
1
3 
 1 3 || - 3 -1 -
1
3 
 0 
cot || 0 -
1
3 
 -1 - 3 || 3 1 
1
3 
 0 -
1
3 
 -1 - 3 || 
2) Giá trị lượng giác của các góc có liên quan đặc biệt 
Góc đối nhau Góc bù nhau Góc phụ nhau 
Góc hơn kém  
Góc hơn kém 
2

cos( ) cos   
sin( ) sin    sin cos
2

 
 
  
 
 sin( ) sin     sin cos
2

 
 
  
 
sin( ) sin    
cos( ) cos    
cos sin
2

 
 
  
 
cos( ) cos     cos sin
2

 
 
   
 
tan( ) tan    
tan( ) tan    
tan cot
2

 
 
  
 
tan( ) tan    tan cot
2

 
 
   
 
cot( ) cot    
cot( ) cot    
cot tan
2

 
 
  
 
cot( ) cot    
cot tan
2

 
 
   
 
Nguyễn Hoài Nam 0979160543 Dạy kèm học sinh từ L6 – L12 
3) Công thức lượng giác 
1) Công thức cộng: 
 cos(a + b) = cosa.cosb – sina.sinb 
 cos(a - b) = cosa.cosb + sina.sinb 
 tan(a - b) = 
tana - tanb
1 + tana.tanb
 sin(a - b) = sina.cosb - cosa.sinb 
 tan(a + b) = 
tana + tanb
1 - tana.tanb
 sin(a + b) = sina.cosb + cosa.sinb 
2) Công thức nhân đôi : 
 sin2x = 2sinxcosx = (sinx+cox)2 - 1 
 cos2x = cos2x – sin2x = 2cos2x - 1 = 1 – 2sin2x 
 tan2x = 
2
2
1
tanx
tan x
 cot2x = 
2 1
2
cot x
cotx

3) Công thức nhân 3: 
 3cos3 4cos 3cosx x x= - 
 3sin3 3sin 4sinx x x= - 
 
3
2
3tan tan
tan3
1 3tan
x x
x
x
-
=
-
 
3
2
3cot cot
cot3
1 3cot
x x
x
x
-
=
-
4) Công thức hạ bậc: 
 2
1 2
os
2
cos x
c x

 
 2
1 os2
sin
2
c x
x

 
 2
1 cos2
tan
1 cos2






 2
1 cos2
cot
1 cos2






 3
1
sin (3sin sin 3 )
4
x x x= - 
 3
1
cos (cos3 3cos )
4
x x x= + 
5) Công thức tích thành tổng. 
 cosxcosy=  
1
( ) ( )
2
cos x y cos x y   
 sinxcosy=  )()(
2
1
yxSinyxSin  
 sinxsiny=  
1
( ) ( )
2
cos x y cos x y    
 [ ]
1
cos .sin sin( ) sin( )
2
x y x y x y= + - - 
6) Công thức tổng(hiệu) thành tích: 
 sinx + siny = 2sin
2 2
x y x y
cos
    
   
   
 sinx – siny = 2 os
2 2
x y x y
c sin
    
   
   
 cosx + cosy = 2cos
2 2
x y x y
cos
    
   
   
 cosx–cosy = 2sin
2 2
x y x y
sin
    
    
   
 tanx + tany = 
( )
cos
sin x y
xcosy

 tanx – tany = 
( )
cos
sin x y
xcosy

 cotx + coty = 
( )
sin
sin x y
xsiny

 cotx – coty = 
( )
sin
sin y x
xsiny

Nguyễn Hoài Nam 0979160543 Dạy kèm học sinh từ L6 – L12 
 
sinx
tanx= ,(x k )
cosx 2

   
 
cosx
cotx= ,(x k )
sinx
  
 
2 2sin x cos x 1  
 
2
2
1
1 tan x,(x k )
2cos x

    
 
2
2
1
1 cot x,(x k )
sin x
   
 ktanx.cotx=1,(x )
2

 
 
3 3sin os (sinx cos )(1 sinx.cos )x c x x x    
 
3 3sin os (sinx cos )(1 sinx.cos )x c x x x    
 4 4 2
1 3 1cos4
sin cos 1 sin 2
2 4
x
x x x

    
 6 6 2
3 cos4
sin cos 1 sin 2
3
84
5 x
x x x

    
  
2
1 sin2 sin cosx x x  
 
sin cos 2 2
4 4
x x sin x cos x
    
       
    
 
sin cos 2 2
4 4
x x sin x cos x
    
        
    
4) Phương trình lượng giác 
a) Phương trình lượng giác cơ bản 
 Dạng: 
 é = a + pê= a Û ê = p - a + pêë
x k2
sin x sin
x k2
 Đặc biệt: 
sin x 0 x k
sin x 1 x k2
2
sin x 1 x k2
2
ìïï = Þ = pïïïï pï = Þ = + pí
ïïï pïï = - Þ = - + pïïî
 Dạng: 
 é = a + pê= a Û ê = - a + pêë
x k2
cos x cos
x k2
 Đặc biệt: 
ìï pï = Þ = + pïïïï = Þ = pí
ïï = - Þ = p + pïïïïî
cos x 0 x k
2
cos x 1 x k2
cos x 1 x k2
 Dạng: 
= a Û = a + p
p
a ¹ + p
t an x tan x k
Ðk : x, k
2
 Đặc biệt: 
 t an x 0 x k
tan x 1 x k
4
ìï = Û = pïï
í pï = ± Û = ± + pïïïî 
 Dạng: 
= a Û = a + p
a ¹ p
cot x cot x k
Ðk : x, k
 Đặc biệt: 
 cot x 0 x k
2
cot x 1 x k
4
ìï pï = Û = + pïïï
í
ï pï = ± Û = ± + pïïïî
+) 
arcsin + 2
sin ,
sin + 2
x a k
x a k
x arc a k

 

    
 +) tan arc tan + ,x a x a k k    
+) 
arc os + 2
os ,
os + 2
x c a k
c x a k
x arcc a k



    
 +) ot ar ot a+ ,c x a x cc k k    
Nguyễn Hoài Nam 0979160543 Dạy kèm học sinh từ L6 – L12 
 Bài 1: Giải các phương trình sau: 
a) 2cos 3 0x - = e) 0
2
s n(x-60 )
2
i
-
= i) sin(3x 1) sin(x- 2) n) 2 cot 0sin x x= 
b) 3 tan 3 3 0x - = f) 0
3
(2x+50 )
2
cos = k)cos3x sin 2x o)sin3 sin5 0x x+ = 
c) 
3
s nx+ 0
2
i = g) tan(2 1) 3x - = l) (1 2 )(4 cos ) 0cox x- - = p) tanxtan2x= -1 
d) s n2x 1i = h) cot(2 ) 1
3
x
p
- = m) (cot 1)(cot 1) 0
3 2
x x
- + = q) 2sin 0x= 
r) 2cos( 2 ) 0x x- = 
b) Phương trình bậc nhất, bậc hai đối với một hàm số lượng giác 
 Phương trình bậc nhất đối với một hàm số lượng giác: để giải các phương trình này ta dùng các công 
thức lượng giác để đưa phương trình về phương trình lượng giác cơ bản. 
 Phương trình bậc hai đối với một hàm số lượng giác: là những phương trình có dạng a.sin2x+b.sinx+c=0 
(hoặc a.cos2x+b.cosx+c=0, a.tan2x+b.tanx+c=0, a.cot2x+b.cotx+c=0) để giải các phương trình này ta đặt t 
bằng hàm số lượng giác.(Chú ý điều kiện của t khi đặt t=sinx hoặc t=cosx) 
Dạng 
Đặt ẩn phụ 
Điều kiện 
2a sin x b sin x c 0+ + = t sin x= 1 t 1- £ £ 
2a cos x b cos x c 0+ + = t cos x= 1 t 1- £ £ 
2a tan x b tan x c 0+ + = t tan x= 
 x k , (k )
2
p
¹ + p Î ¢ 
2a cot x b cot x c 0+ + = =t cot x ( )¹ p Î ¢x k , k 
Nếu đặt 2t sin x= hoặc t sin x= thì điều kiện là 0 t 1£ £ 
Một số hằng đẳng thức lượng giác và mối liên hệ 
 
( )
2
2 21 sin 2x sin x cos x 2sin x cos x sin x cos x+ = + + = +
 
( )
2
2 21 sin 2x sin x cos x 2sin x cos x sin x cos x- = + - = -
 
sin 2x
sin x cos x
2
=
 
( )( )3 3sin x cos x sin x cos x 1 sin x cos x+ = + -
 
( )( )x3 3sin x cos x sin x cos x 1 sin x cos- = - +
Nguyễn Hoài Nam 0979160543 Dạy kèm học sinh từ L6 – L12 
 
2 2sin x cos x sin x cos x 2
tan x cot x
cos x sin x sin x cos x sin 2x
+
+ = + = =
 
2 2cos x sin x cos x sin x 2cos2x
cot x tan x 2cot x
sin x cos x sin x cos x sin 2x
-
- = - = = =
 
4 4 2 21 1 1 3 1cos 4xsin x cos x 1 sin 2x cos 2x
2 2 2 4
+
+ = - = + =
 
( )( )4 4 2 2 2 2cos x sin x sin x cos x cos x sin x cos2x- = + - =
 
6 6 4 4 2 2 23 5 3cos 4xsin x cos x sin x cos x sin x cos x 1 sin 2x
4 8
+
+ = + - = - =
 
( )6 6 4 4 2 2cos x sin x cos2x sin x cos x sin x cos x- = + +
 
x 1
1 tan x tan
2 cos x
+ =
 
sin x cos x 2 sin x 2 cos x
4 4
æ ö æ öp p÷ ÷ç ç÷ ÷± = ± =ç ç÷ ÷ç ç÷ ÷ç çè ø è ø
m
 
( ) ( )
2 2cos x cos x 1 sin x 1 sin x
1 sin x cos xcos x 1 sin x cos x 1 sin x
- +
= = =
- - -
 (mối liên hệ giữa sinx và cosx) 
Bài 2: Giải các phương trình sau: 
a) 22cos 3cos 1 0x x- + = k) ( )
æ ö æ öp p÷ ÷ç ç÷ ÷+ + - + = + -ç ç÷ ÷ç ç÷ ÷ç çè ø è ø
cos 2x cos 2x 4 sin x 2 2 1 sin x
4 4
b) 2 22cos 2 3sin 2x x+ = l) - =5 5 24sin x cosx 4cos x sin x sin 4x 
c) 23cos 2sin 2 0x x- + = m) cos 3cos 2 0
2
x
x+ + = 
d) 25sin 3cos 3 0x x+ + = n) 
2cot 2x+3cot2x+2=0 
e) 22sin 3sinx-5 0x+ = o)  22cos 2x 2 3 1 cos2x 3 0    
f) tanx+cotx=2 p)  2 23cot 2 2 sin 2 3 2 osxx x c   
g) 23sin 2x 4cos2x 4 0   q)  2tan x 3 1 tan x 3 0    
h) 2 2sin x 2sin 2x 1  r)  22cos 2x 2 3 1 cos2x 3 0    
i) 
2
4
tanx 7
cos x
  t) 
( )+ -
=
-
6 62 cos x sin x sin x cos x
0
2 2 sin x
j) 2(tanx+cotx) -(tanx+cotx)=2 s) 
( )
æ öp÷ç ÷+ + +ç ÷ç ÷è ø
=
+
1 sin x cos2x sin x
4 1
cos x
1 tan x 2
Nguyễn Hoài Nam 0979160543 Dạy kèm học sinh từ L6 – L12 
c) Phương trình bậc nhất đối với sinx và cosx: 
Dạng: asinx+bcosx=c. Điều kiện để phương trình có nghiệm là 2 2 2a b c  . 
Cách 1: asinx+bcosx=c 
 Đặt: 
2 2
cos
a
a b
 

 ; 
2 2
sin
b
a b
 

2 2 sin( )a b x c    
Cách 2: sin cos
b
a x x c
a
 
  
 
Đặt:  tan sin cos .tan
b
a x x c
a
     sin( ) cos
c
x
a
    
Cách 3: Đặt: tan
2
x
t  ta có: 
2
2 2
2 1
sin ;cos
1 1
t t
x x
t t

 
 
 2( ) 2 0b c t at b c      
Bài 3: Giải các phương trình sau: 
a) 3sinx cos 1x- = h) sin2x cos2x 1  
b) 2sin 3 5 cos3 3x x+ = - i)  sin8x cos6x 3 sin6x cos8x   
c) 
3
sin3x cos3x
2
  j) 2 2sin x sin 2x 3cos x  
d) 3sin5x 2cos5x 3  k) 
3 2
2sin( ) sin( )
4 4 2
x x
p p
+ + - = 
e) 4sin x cosx 4  l) 
1
4sin 3cos 4(1 tan )
cos
x x x
x
+ = + - 
f) sin2x cos2x 1  m) 
æ ö÷ç ÷+ = =ç ÷ç ÷çè ø
2
x x
sin cos 3 cos x 2
2 2
g)    sin x 1 sin x cosx cosx 1   n) 
æ öp p÷ç ÷- = - " Î ç ÷ç ÷çè ø
2 6
cos7x 3 sin 7x 2 , x ;
5 7
d) Phương trình lượng giác đẳng cấp 
 Dạng: ( ) + + = " Î ¡2 2a.sin X b.sin x cos x c.cos x d 1 a, b, c, d 
Cách 1: 
 Bước 1. Kiểm tra xem ( ) ( ) x
ìï =p ïï= + p Î Û = pí
ï =ïïî
¢
2
cos x 0
x k , k Hay k
sin x 12
 có phải là nghiệm của 
phương trình ( )1 hay không ? Nếu phải thì nhận nghiệm này. 
 Bước 2. Khi ( ) ( ) x
ìï ¹p ïï¹ + p Î Û ¹ pí
ï ¹ïïî
¢
2
cos x 0
x k , k Hay k
sin x 12
 . Chia hai vế của ( )1 cho 2cos x 
(hay 2sin x ), ta được: 
Nguyễn Hoài Nam 0979160543 Dạy kèm học sinh từ L6 – L12 
( )Û + + =
2 2
2 2 2 2
sin x sin x cos x cos x d
1 a. b. c.
cos x cos x cos x cos x
( ) Û + + = +2 2a tan x b tan x c d 1 tan x 
 Bước 3: Đặt =t tan x để đưa về phương trình bậc hai đã biết cách giải. 
Cách 2: Sử dụng công thức hạ bậc và nhân đôi 
 Bước 1: Thế 
- +
= =2 2
1 cos2x 1 cos2x
sin x ; cos x
2 2
 và =
sin 2x
sin x cos x
2
 vào ( )1 và rút gọn lại, 
ta được: ( ) ( ) + - = - - *b sin 2x c a cos2x 2d a c 
 Bước 2: Giải phương trình ( )* , tìm nghiệm. Đây là phương trình bậc nhất đối với sin 2x và 
cos2x mà đã biết cách giải. 
 Dạng: 
( )
( )
é + + + =ê
ê
+ + + + =êë
3 2 2 3
4 3 2 2 3 4
a. sin x b. sin x cos x c. sin x cos x d.cos x 0 2
a. sin x b. sin x cos x c. sin x cos x d. sin x cos x e.cos x 0 3
Cách giải: Chia hai vế của ( )2 cho 3cos X (hay 3sin X ) hoặc chia hai vế của ( )3 cho 
4cos X (hay 4sin X ) và giải tương tự như trên. 
Bài 4: Giải phương trình lượng giác: 
a) - = +2 2cos x 3 sin 2x 1 sin x 
b) + - + - =2 22sin x (1 3)sin x cosx (1 3)cos x 1 
c) - - =2 24sin x 5sin x cosx 6cos x 0 
d) - + =2 2sin x 3 sin x cosx 2cos x 1 
e) + - =2 22sin x 3 3 sin x cosx cos x 4 
f) + + - =2 23sin x 4sin 2x (8 3 9)cos x 0 
g) + - =2 2
1
sin x 2sin x cos x 2cos x
2
h) - + + =2 2sin x 3sin x cos x 4cos x 3 
i) - - =2 22sin x cos x sin x cosx 2 
j) + - =2 24sin x 3cos x 4sin x cos x 1 
k) + - =2 23sin x 4cos x 3sin x cos x 1 
l) + + =2 25sin x cos x sin 2x 2 
( )Û - + + - =2a d tan x b tan x c d 0 
Nguyễn Hoài Nam 0979160543 Dạy kèm học sinh từ L6 – L12 
e) Phương trình lượng giác đối xứng 
Dạng 1. 
( )a sin x cos x b sin x cos x c 0+ + + = 
2t 1
PP : t sin x cos x, t 2 sin x cos x
2
-
Þ = + £ Þ =
Dạng 2. 
( )a sin x cos x b sin x cos x c 0- + + = 
21 t
PP : t sin x cos x, t 2 sin x cos x
2
-
Þ = - £ Þ =
Dạng 3. 
( ) ( )2 2a tan x cot x b tan x cot x c 0+ + + + =
( )
sin x 0 k
ÐK : sin 2x 0 x , k
cos x 0 2
ìï ¹ pï Û ¹ Û ¹ Îí
ï ¹ïî
¢
 2 2 2PP : t tan x cot x , t 2 tan x cot x t 2Þ = + ³ Þ + = -
Dạng 4. 
( ) ( )2 2a tan x cot x b tan x cot x c 0+ + - + =
( )
sin x 0 k
ÐK : sin 2x 0 x , k
cos x 0 2
ìï ¹ pï Û ¹ Û ¹ Îí
ï ¹ïî
¢
 2 2 2PP : t tan x cot x , t 2 tan x cot x t 2Þ = - ³ Þ + = +
Dạng 5. 
( )4 4a sin x cos x b sin 2x c 0+ + + =
 4 4 2 2
1 1
PP : t sin 2x, t 1 sin x cos x 1 sin 2x 1 t
2 2
Þ = £ Þ + = - = -
Dạng 6. 
( )4 4a sin x cos x b cos2x c 0+ + + =
 4 4 2 2 2
1 1 1 1 1
PP : t cos2x, t 1 sin x cos x 1 sin 2x cos 2x t
2 2 2 2 2
Þ = £ Þ + = - = + = +
Dạng 7. 
( )6 6a sin x cos x b sin 2x c 0+ + + =
 6 6 2 2
3 3
PP : t sin 2x, t 1 sin x cos x 1 sin 2x 1 t
4 4
Þ = £ Þ + = - = -
Dạng 8. 
( )6 6a sin x cos x b cos2x c 0+ + + =
 6 6 2 2 2
3 1 3 1 3
PP : t cos2x, t 1 sin x cos x 1 sin 2x cos 2x t
4 4 4 4 4
Þ = £ Þ + = - = + = +
Dạng 9. 
4 4a sin x b cos x ccos2x d 0+ + + = 
( )
( )
2
2 4
2
2
4
1 t1 cos2x 1 t
sin x sin x
2 2 4PP : t cos2x, t 1
1 cos2x 1 t 1 tcos x
cos x2 2
4
ìïì ï -ï - - ïï ï= = =ï ïïï ïÞ = £ Þ Þí í
ï ï+ + +ï ï= =ï ï =ï ïïî ïïî
Nguyễn Hoài Nam 0979160543 Dạy kèm học sinh từ L6 – L12 
Bài 5: Giải các phương trình sau: 
a)  2 sin x cosx 6sin xcosx 2 0    k) sin x cosx 4sin xcosx 1 0    
b)  sin xcosx 2 sin x cosx 1 0    l)  6 sin x cosx 1 sin xcosx   
c) sinx cosx 2 6sinxcosx  m)  2 2 sin x cosx 3sin2x  
d)  2sin2x 3 3 sin x cosx 8 0    n) 
1
sin x 2sin2x cosx
2
   
e) + - =
3 3 3sin x cos x 1 sin 2x
2 o) 
+ =3 3cos x sin x cos2x 
f) ( )+ = +2 sin x cosx tan x cot x
 p) 
- =3 3cos x sin x 1 
g) + - =
3 31 cos x sin x sin x
 q) 
( )- - + =sin 2x 12 sin x cos x 12 0 
h) - = +cot x tan x sin x cosx
 r) 
+
=
+
sin x cos x
1
sin 2x 1
i) + = +1 tan x sin x cosx
 s) 
+ + =sin x cosx 2sin x 2cosx 2 
j) 
æ öp ÷ç ÷+ - =ç ÷ç ÷çè ø
sin 2x 2 sin x 1
4
 t) 
+ =6 6sin x cos x sin 2x 
Nguyễn Hoài Nam 0979160543 Dạy kèm học sinh từ L6 – L12 
f) Một số dạng phương trình khác 
 PHƯƠNG TRÌNH LƯỢNG GIÁC CHỨA CĂN VÀ CHỨA TRỊ TUYỆT ĐỐI 
Phương pháp: 
 Phương trình chứa căn thức: Áp dụng công thức 
 ● 
A 0 B 0
A B
A B A B
ì ìï ï³ ³ï ï= Û Ûí í
ï ï= =ï ïî î ● 
2
B 0
A B
A B
ìï ³ïï= Û í
ï =ïïî 
Lưu ý: Khi giải B 0³ , ta áp dụng phương pháp thử lại. 
 Phương trình chứa giá trị tuyệt đối 
 Cách 1. Mở giá trị tuyệt đối dựa vào định nghĩa 
 Cách 2. Áp dụng công thức 
 ● 
A B
A B
A B
é =ê= Û ê = -êë ● 
A 0
B 0
A B
A BA B
A 0
A B
A B
éìï ³ïêìï ³ íêï ï =ï êïï é î== Û Ûí êê ìï ï <êï ê ï= -ï êíêï ëî ïê = -ïîë 
 PHƯƠNG TRÌNH LƯỢNG GIÁC KHÔNG MẪU MỰC 
 Loại 1. Tổng hai số không âm: 
A 0
A 0
B 0
B 0
A B 0
ìï ³ï ìïï =ïï ³ Þí í
ï ï =ï ïî+ =ïïî
 Loại 2. Phương pháp đối lập dạng 1: 
A M
A M
B M
B M
A B
ìï £ï ìïï =ïï ³ Þí í
ï ï =ï ïî=ïïî
 Loại 3. Phương pháp đối lập dạng 2: 
A M
A M
B N
B N
A B M N
ì ìï ï £ï ï ìïï =í ïï ï £ Þí íïîï ï =ï ïîï + = +ïî
 Đặc biệt ● 
sin u 1
sin u sin v 2
sin v 1
ìï =ï± = Û í
ï = ±ïî
 ● 
sin u 1
sin u sin v 2
sin v 1
ìï = -ï+ = - Û í
ï = -ïî
 ● 
cosu 1
cosu cos v 2
cos v 1
ìï =ï± = Û í
ï = ±ïî
 ● 
cosu 1
cosu cos v 2
cos v 1
ìï = -ï+ = - Û í
ï = -ïî
Nguyễn Hoài Nam 0979160543 Dạy kèm học sinh từ L6 – L12 
 ● 
sin u 1
sin v 1
sin u. sin v 1
sin u 1
sin v 1
éìï =ïê
íêï =êïî= Û êìï = -êïêí
ïê = -ïîë
 ● 
sin u 1
sin v 1
sin u. sin v 1
sin u 1
sin v 1
éìï = -ïê
íêï =êïî= - Û êìï =êïêí
ïê = -ïîë
 ● 
cos u 1
cos v 1
cos u.cos v 1
cos u 1
cos v 1
éìï =ïê
íêï =êïî= Û êìï = -êïêí
ïê = -ïîë
 ● 
cos u 1
cos v 1
cos u.cos v 1
cos u 1
cos v 1
éìï = -ïê
íêï =êïî= - Û êìï =êïêí
ïê = -ïîë