Tài liệu ôn thi Đại học môn Đại số
PHƯƠNG TRÌNH LOGARIT
A. CÔNG THỨC CẦN NHỚ
Cho các số a, b và c thỏa điều kiện của lôgarit. Khi đó ta có:
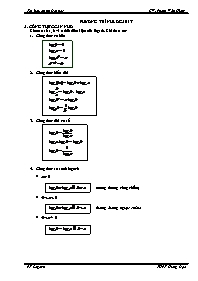
1. Công thức cơ bản
2. Công thức biến đổi
3. Công thức đổi cơ số
4. Công thức so sánh logarit
(tương đương cùng chiều)
(tương đương ngược chiều)
Bạn đang xem tài liệu "Tài liệu ôn thi Đại học môn Đại số", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
PHƯƠNG TRÌNH LOGARIT A. CÔNG THỨC CẦN NHỚ Cho các số a, b và c thỏa điều kiện của lôgarit. Khi đó ta có: Công thức cơ bản Công thức biến đổi Công thức đổi cơ số Công thức so sánh logarit (tương đương cùng chiều) (tương đương ngược chiều) B. PHƯƠNG TRÌNH LOGARIT hoặc I. PHƯƠNG PHÁP ĐƯA VỀ CÙNG CƠ SỐ Chú ý: Tùy theo từng bài mà ta lựa chọn điều kiện hay cho phù hợp. Bài tập: Giải các phương trình sau: a) b) ĐK: Với điều kiện đó phương trình đã cho tương đương với: Kết hợp với điều kiện ta có nghiệm của phương trình là c) ĐK: Với điều kiện đó phương đã cho trình tương đương với: (TM ĐK) d) ĐK: PT cho tương đương với: Cách 1: Cách 2: Sai lầm ở đâu? Hãy sửa lại cho đúng! e) ĐK: PT cho tương đương với: f) ĐK: Với điều kiện , phương trình tương đương với: (loại) (TM) Đặt , ta được phương trình: Với ta được (TM điều kiện ). Vậy phương trình có nghiệm g) (loại) (TM) . Đặt , ta được phương trình: Với . Vậy phương trình có nghiệm h) ĐK: Với điều kiện đó phương trình tương đương với: i) II. PHƯƠNG PHÁP ĐẶT ẨN PHỤ a) ĐK: . Đặt ta được Với Với b) ĐK: Với điều kiện đó phương trình tương đương với: . Đặt ta được phương trình: c) ĐK: Với điều kiện đó phương trình tương đương với: Đặt ta được phương trình: d) ĐK: Với điều kiện đó phương trình tương đương với phương trình: . Đặt ta được: e) ĐK: Với điều kiện đó phương trình tương đương với phương trình: . Đặt ta được phương trình: f) ĐK: Với điều kiện đó phương trình đã cho tương đương với phương trình: . Đặt ta được phương trình: (loại) (TM) Với g) (ĐS: ) h) (ĐS: Vô nghiệm) i) (ĐS: )
Tài liệu đính kèm:
 PT Logarit.doc
PT Logarit.doc





