Bài tập trắc nghiệm môn Toán Lớp 11 (Có đáp án) - Chủ đề 1: Hàm số lượng giác và phương trình lượng giác
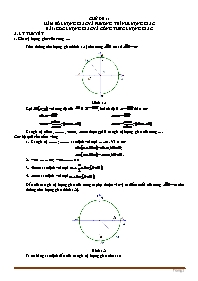
1. Giá trị lượng giác của cung
Trên đường tròn lượng giác (hình 1.1) cho cung có sđ :
Các giá trị , , , được gọi là các giá trị lượng giác của cung .
Các hệ quả cần nắm vững
1. Các giá trị ; xác định với mọi . Và ta có:
3. xác định với mọi .
4. xác định với mọi .
Dấu của các giá trị lượng giác của cung phụ thuộc vào vị trí điểm cuối của cung trên đường tròn lượng giác (hình 1.2).
Bạn đang xem 20 trang mẫu của tài liệu "Bài tập trắc nghiệm môn Toán Lớp 11 (Có đáp án) - Chủ đề 1: Hàm số lượng giác và phương trình lượng giác", để tải tài liệu gốc về máy bạn click vào nút DOWNLOAD ở trên
CHỦ ĐỀ 1: HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC BÀI: GÓC LƯỢNG GIÁC VÀ CÔNG THỨC LƯỢNG GIÁC A. LÝ THUYẾT 1. Giá trị lượng giác của cung . Trên đường tròn lượng giác (hình 1.1) cho cung có sđ : Hình 1.1 Gọi với tung độ của là , hoành độ là thì ta có: Các giá trị , , , được gọi là các giá trị lượng giác của cung . Các hệ quả cần nắm vững Các giá trị ; xác định với mọi . Và ta có: ; xác định với mọi . xác định với mọi . Dấu của các giá trị lượng giác của cung phụ thuộc vào vị trí điểm cuối của cung trên đường tròn lượng giác (hình 1.2). Hình 1.2 Ta có bảng xác định dấu của các giá trị lượng giác như sau Góc phần tư Giá trị lượng giác I II III IV + - - + + + - - + - + - + - + - Ở hình 1.3 là một cách nhớ khác để xác định dấu của các giá trị lượng giác 2. Công thức lượng giác Công thức cơ bản Cung đối nhau Công thức cộng Cung bù nhau Công thức đặc biệt Góc nhân đôi Góc chia đôi Góc nhân ba Góc chia ba STUDY TIP Ở đây từ các công thức góc nhân đôi, góc nhân ba ta có thể suy ra công thức góc chia đôi, chia ba mà không cần nhớ nhiều công thức. Biến đổi tích thành tổng Biến đổi tổng thành tích 3. Giá trị lượng giác của các cung đặc biệt (độ) 0 (radian) 0 0 1 0 1 0 0 1 Không xác định 0 STUDY TIP Từ bảng giá trị lượng giác các cung đặc biệt ở bên ta thấy một quy luật như sau để độc giả có thể nhớ các giá trị lượng giác của các cung đặc biệt: Các giá trị ở tử số tăng dần từ đến . Ngược lại đối với giá trị , tử số giảm dần từ về . BÀI: HÀM SỐ LƯỢNG GIÁC A. LÝ THUYẾT 1. Hàm số và hàm số . Quy tắc đặt tương ứng mỗi số thực với của góc lượng giác có số đo rađian bằng được gọi là hàm số , kí hiệu là . Quy tắc đặt tương ứng mỗi số thực với của góc lượng giác có số đo rađian bằng được gọi là hàm số , kí hiệu là . Tập xác định của các hàm số là . Hàm số Nhận xét: Hàm số là hàm số lẻ do hà số có tập xác định là đối xứng và Hàm số tuần hoàn với chu kì . Sự biến thiên: Sự biến thiên của hàm số trên đoạn được biểu thị trong sơ đồ (hình 1.4) phía dưới: Bảng biến thiên: Từ đây ta có bảng biến thiên của hàm số trên đoạn như sau: STUTY TIP Khái niệm: Hàm số xác định trên gọi là hàm tuần hoàn nếu tồn tại một số sao cho với mọi thuộc ta có . Số dương nhỏ nhất (nếu có) thỏa mãn tính chất trên gọi là chu kì của hàm tuần hoàn. Đồ thị hàm số: Nhận xét: Do hàm số là hàm số lẻ trên và tuần hoàn với chu kì nên khi vẽ đồ thị hàm số trên ta chỉ cần vẽ đồ thị hàm số trên đoạn , sau đó lấy đối xứng đồ thị qua gốc tọa , ta được đồ thị hàm số trên đoạn , cuối cùng tịnh tiến đồ thị vừa thu được sang trái và sang phải theo trục hoành ta được các đoạn có độ dài STUDY TIP Hàm số đồng biến trên khoảng . Do tính chất tuần hoàn với chu kì , hàm số đồng biến trên mỗi khoảng . Tương tự ta suy ra được hàm số nghịch biến trên mỗi khoảng GHI NHỚ Hàm số - Có tập xác định là . - Có tập giá trị là . - Là hàm số lẻ. - Đồ thị nhận gốc tọa độ làm tâm đối xứng. - Có đồ thị là một đường hình sin. - Tuần hoàn với chu kì . - Đồng biến trên mỗi khoảng . - Nghịch biến trên mỗi khoảng . Hàm số Ta thấy nên bằng cách tịnh tiến đồ thị hàm số sang trái một đoạn có độ dài , ta được đồ thị hàm số . Bảng biến thiên của hàm số trên . Đồ thị hàm số : STUTY TIP Hàm số đồng biến trên khoảng . Do tính chất tuần hoàn với chu kì , hàm số đồng biến trên mỗi khoảng . Tương tự ta suy ra được hàm số nghịch biến trên mỗi khoảng . GHI NHỚ Hàm số : - Có tập xác định là . - Là hàm số chẵn. - Là một đường hình sin. - Đồng biến trên mỗi khoảng . - Nghịch biến trên mỗi khoảng . Đọc thêm Hàm số là một hàm tuần hoàn với chu kì cơ sở vì: Và đồ thị của nó cũng là một đường hình sin. Tương tự hàm số cũng là một hàm tuần hoàn với chu kì cơ sở và đồ thị của nó cũng là một đường hình sin. Ứng dụng thực tiễn: Dao động điều hòa trong môn Vật lý chương trình 12. 2. Hàm số và hàm số Hình 1.7 Với , quy tắc đặt tương ứng mỗi số với số thực được gọi là hàm số tang, kí hiệu là . Hàm số có tập xác định là . Với , quy tắc đặt tương ứng mỗi số với số thực được gọi là hàm số côtang, kí hiệu là . Hàm số có tập xác định là . Nhận xét: - Hai hàm số và hàm số là hai hàm số lẻ. - Hai hàm số này là hai hàm số tuần hoàn với chu kì . a) Hàm số Hình 1.8 Sự biến thiên: Khi cho tăng từ đến thì điểm chạy trên đường tròn lượng giác theo chiều dương từ đến (không kể và ). Khi đó điểm thuộc trục tang sao cho chạy dọc theo , nên tăng từ đến (qua giá trị khi ). Giải thích: vì Nhận xét: Hàm số đồng biến trên mỗi khoảng . Đồ thị hàm số nhận mỗi đường thẳng làm một đường tiệm cận. Đồ thị hàm số: Nhận xét: Do hàm số là hàm số lẻ trên và tuần hoàn với chu kì nên khi vẽ đồ thị hàm số trên ta chỉ cần vẽ đồ thị hàm số trên , sau đó lấy đối xứng đồ thị qua gốc tọa độ , ta được đồ thị hàm số trên , cuối cùng tịnh tiến đồ thị vừa thu được sang trái và sang phải theo trục hoành. Hình 1.9 STUDY TIP Hàm số nhận mỗi đường thẳng làm một đường tiệm cận GHI NHỚ Hàm số : - Có tập xác định - Là hàm số lẻ - Là hàm số tuần hoàn với chu kì - Có tập giá trị là - Đồng biến trên mỗi khoảng - Đồ thị nhận mỗi đường thẳng làm một đường tiệm cận b) Hàm số Hàm số có tập xác định là một hàm số tuần hoàn với chu ki . Tương tự khảo sát như đối với hàm số ở trên thì ta có thể vẽ đồ thị hàm số như sau: Hình 1.10 GHI NHỚ Hàm số : - Có tập xác định: - Là hàm số lẻ - Là hàm số tuần hoàn với chu kì - Có tập giá trị là - Đồng biến trên mỗi khoảng - Đồ thị nhận mỗi đường thẳng làm một đường tiệm cận. B. Các dạng toán liên quan đến hàm số lượng giác Dạng 1: Bài toán tìm tập xác định của hàm số lượng giác Cách 1 Tìm tập của để có nghĩa, tức là tìm . Cách 2 Tìm tập của để không có nghĩa, khi đó tập xác định của hàm số là . CHÚ Ý A. Với hàm số cho bởi biểu thức đại số thì ta có: 1. , điều kiện: * có nghĩa * có nghĩa và . 2. , điều kiện: có nghĩa và . 3. , điều kiện: có nghĩa và . B. Hàm số xác định trên , như vậy xác định khi và chỉ khi xác định. * có nghĩa khi và chỉ khi xác định và . * có nghĩa khi và chỉ khi xác định và . STUDY TIP Ở phần này chúng ta chỉ cần nhớ kĩ điều kiện xác định của các hàm số cơ bản như sau: 1. Hàm số và xác định trên . 2. Hàm số xác định trên . 3. Hàm số xác định trên . Tập xác định của hàm số là: A. . B. . C. . D. . Chọn A. Lời giải Cách 1: Hàm số đã cho xác định khi . Cách 2: Sử dụng máy tính cầm tay tính giá trị của hàm số tại và ta thấy hàm số đều không xác định, từ đây ta chọn A. STUDY TIP Đối với hàm côsin, trong một chu kỳ tuần hoàn của hàm số tồn tại hai góc có số đo là và cùng thỏa mãn chính vì thế ta kết luận được điều kiện như vậy. Cách bấm như sau: Nhập vào màn hình : Ấn r gán thì máy báo lỗi, tương tự với trường hợp . Từ đây suy ra hàm số không xác định tại và . Tập xác định của hàm số là: A. . B. . C. . D. . Chọn C. Lời giải Hàm số đã cho xác định khi + xác định + . STUDY TIP Trong bài toán này, nhiều độc giả có thể chỉ sử dụng điều kiện để hàm phân thức xác định chứ không chú ý điều kiện để hàm xác định, sẽ bị thiếu điều kiện và chọn D là sai. Tập hợp không phải là tập xác định của hàm số nào? A. . B. . C. . D. . Chọn C. Lời giải Phân tích: Với các bài toán dạng này nếu ta để ý một chút thì sẽ thấy hàm xác định với mọi . Nên ta chỉ xét mẫu số, ở đây có đến ba phương án có mẫu số có chứa như nhau là và . Do đó ta chọn được luôn đáp án Trong ví dụ trên ta có thể gộp hai họ nghiệm và thành dựa theo lý thuyết sau: Hình 1.11 Mỗi cung (hoặc góc) lượng giác được biểu diễn bởi một điểm trên đường tròn lượng giác được biểu diễn bởi một điểm trên đường tròn lượng giác. được biểu diễn bởi hai điểm đối xứng nhau qua trên đường tròn lượng giác. được biểu diễn bởi ba điểm cách đều nhau, tạo thành đỉnh của một tam giác đều nội tiếp đường tròn lượng giác. được biểu diễn bởi điểm cách đều nhau, tạo thành đỉnh của một đa giác đều nội tiếp đường tròn lượng giác. Giải thích cách gộp nghiệm ở ví dụ 3 ta có Trên hình 1.11 hai chấm tròn đen là điểm biểu diễn hai nghiệm ta tìm được ở ví dụ 3. Từ đây nếu gộp nghiệm lại thì ta sẽ có . Tìm tập xác định của hàm số A. . B. . C. . D. . Lời giải Chọn D. Hàm số đã cho xác định khi xác định STUDY TIP Ở đây nhiều độc giả nhầm lẫn, thấy hàm số và chọn luôn là sai. Cần chú ý đến điều kiện để xác định. Tập xác định của hàm số là A. . B. . C. . D. . Lời giải Chọn D. Ta có 2017 là một số nguyên dương, do vậy hàm số đã cho xác định khi xác định . STUDY TIP Trong bài này, ta cần thêm kiến thức về tập xác định của hàm số lũy thừa ở lớp 12: Tập xác định của hàm số tùy thuộc vào giá trị của * Với nguyên dương thì tập xác định là . * Với nguyên âm hoặc bằng , tập xác định là . * Với không nguyên, tập xác định là . Tập xác định của hàm số là A. . B. . C. . D. . Lời giải Chọn B. Tương tự như ví dụ 5, ta có hàm số xác định khi xác định . Tập xác định của hàm số là A. . B. . C. . D. . Lời giải Chọn B. Hàm số xác định khi Mặt khác ta có nên . STUDY TIP Với các bài toán chứa căn thức ta chú ý các hệ số tự do để áp dụng các bất đẳng thức cơ bản như Tập xác định của hàm số là A. . B. . C. . D. . Lời giải Chọn B. Ta có ,. Vậy hàm số đã cho xác đinh với mọi . Một dạng khác của bài toán liên quan đến tìm tập xác định của hàm lượng giác như sau: Để tìm tập xác định của hàm số , một học sinh đã giải theo các bước sau: Bước 1: Điều kiện để hàm số có nghĩa là . Bước 2: . Bước 3: Vậy tập xác định của hàm số đã cho là . Bài giải của bạn đó đúng chưa? Nếu sai, thì sai bắt đầu ở bước nào? A. Bài giải đúng. B. Sai từ bước 1. C. Sai từ bước 2. D. Sai từ bước 3. Lời giải Chọn B. Nhận thấy hàm số đã cho xác định khi xác định (do xác định với mọi ). Do vậy hàm số xác định khi . Hàm số xác định khi và chỉ khi A. . B. . C. . D. . Lời giải Chọn A. Hàm số đã cho xác định (do ). Dạng chứa tham số trong bài toán liên quan đến tập xác định của hàm sô lượng giác. Với (là tập xác định của hàm số ) thì . . . Cho hàm số .Tất cả các giá trị của tham số để hàm số xác định với mọi số thực (trên toàn trục số) là A. . B. . C. . D. . Lời giải Chọn A. Xét hàm số . Đặt . Hàm số xác định với mọi . Đặt trên . Đồ thị hàm số có thể là một trong ba đồ thị trên. Ta thấy hoặc Ycbt . Tìm để hàm số xác định trên . A. . B. . C. . D. . Lời giải Chọn B. Hàm số xác định trên khi và chỉ khi . Đặt Lúc này ta đi tìm điều kiện của để Ta có TH 1: . Khi đó (thỏa mãn). TH 2: (thử lại thì cả hai trường hợp đều không thỏa mãn). TH 3: khi đó tam thức có hai nghiệm phân biệt . Để thì . Vậy thỏa mãn yêu cầu bài toán. Chú ý: Với các bài toán dạng này ta cần chia ba ... . D. . Lời giải Chọn B. Phương trình -Giải (1) , các nghiệm này không thuộc . -Giải (2) có Suy ra phương trình (2) có nghiệm thuộc Vậy có 1 giá trị nguyên của là Phương trình nhận các giá trị làm nghiệm thì giá trị là: A. . B. . C. D. . Lời giải Chọn B. Phương trình Vậy STUDY TIP Phương trình là phương trình hệ quả của phương trình: A. B. C. D. Lời giải Chọn C pt Lưu ý: Phương trình bậc hai có hai nghiệm thì VI. MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC CHỨA ĐIỀU KIỆN Phương trình có số nghiệm là: A. 0 B. 1 C. 2 D. vô số Lời giải Chọn A Điều kiện: Với (loại vì không TMĐK) Vậy phương trình đã cho vô nghiệm Phương trình có các nghiệm dạng thì bằng: A. B. - C. D. Lời giải Chọn A Điều kiện: Vậy Phương trình có tổng các nghiệm trên là: A. B. C. D. Lời giải Chọn D Điều kiện: =>có 2 nghiệm trên là x= và x= Vậy tổng các nghiệm trên là: Phương trình có bao nhiêu nghiệm trên? A. 1 B. 2 C. 3 D. 4 Lời giải Chọn B Điều kiện: Kết hợp điều kiện (*)=>Nghiệm của phương trình là Vậy có hai nghiệm thuộc là và Phương trình có các nghiệm dạng thì là: A. B. C. D. Lời giải Chọn C Điều kiện: Kết hợp điều kiện(*) ta có nghiệm của pt là Phương trình có số điểm biểu diễn nghiệm trên đường tròn lượng giác là: A. 2 B. 4 C. 6 D. 8 Lời giải Chọn B Điều kiện: Ta có: . . Kết hợp điều kiện ⇒ nghiệm của phương trình (1) là Vậy số điểm biểu diễn cần tìm là 4. Lưu ý: Ở bài nầy điều kiện bài toán có thể gộp thành Bài tập rèn luyện kỹ năng Phương trình lượng giác cơ bản Phương trình có nghiệm là: A. và B. và C. và D. và Số nghiệm của phương trình với là: A. B. C. D. Phương trình có nghiệm khi: A. B. C. D. Phương trình có nghiệm khi: A. B. C. D. Phương trình có nghiệm là: A. B. C. D. Tổng các nghiệm của phương trình trên khoảng là: A. B. C. D. Phương trình nào sau đây tương đương với phương trình ? A. B. C. D. Phương trình Có các nghiệm dạng và Khi đó bằng A. B. C. D. Phương trình có bao nhiêu nghiệm thuộc A. B. C. D. Nghiệm âm lớn nhất của phương trình A. B. C. D. Trong các phương trình sau, phương trình nào vô nghiệm? A. B. C. D. Một số phương trình lượng giác thường gặp Số nghiệm của phương trình Trên đoạn A. B. C. D. 4 Phương trình Có nghiệm khi A. . C. D. Có bao nhiêu giá trị nguyên của m để phương trình Có nghiệm? A. B. C. D. Vô số Tổng các nghiệm của phương trình trên khoảng A. B. C. D. Phương trình có nghiệm dạng thì giá trị m là: A. B. C. D. Tổng 2 nghiệm dương liên tiếp nhỏ nhất của phương trình: là: A. B. C. D. Nghiệm của phương trình là: A. B. C. D. Nghiệm của phương trình là: A. . B. . C. . D. . Phương trình có bao nhiêu điểm biểu diễm trên đường tròn lượng giác? A. . B. . C. . D. . Có bao nhiêu giá trị nguyên của để phương trình có hai nghiệm thuộc ? A. . B. . C. Vô số. D. Không có . Giá trị của để phương trình có nghiệm trên là thì là: A. . B. . C. . D. . Phương trình có tổng nghiệm âm lớn nhất liên tiếp là: A. . B. . C. . D. . Phương trình có nghiệm khi thì tích bằng: A. . B. . C. . D. . Phương trình có các nghiệm dạng và ; thì: A. . B. . C. . D. . Cho các phương trình sau:. . . . Trong các phương trình trên, phương trình nào vô nghiệm A. Chỉ phương trình (1) vô nghiêm. B. Chỉ phương trình (2) vô nghiệm. C. Chỉ phương trình (3) vô nghiệm. D. Cả phương trình vô nghiệm. Phương trình bậc nhất đối với , . Phương trình có nghiệm khi: A. . B. . C. . D. . Phương trình có các nghiệm dạng và , với thì là: A. . B. . C. . D. . Phương trình có các nghiệm là: A. . B. . C. . D. . Phương trình có tổng hai nghiệm dương nhỏ nhất liên tiếp là: A. . B. . C. . D. . Phương trình có nghiệm dương nhỏ nhất là và nghiệm âm lớn nhất là thì là: A. . B. . C. . D. . Phương trình đẳng cấp bậc hai. Số điểm biểu diễn nghiệm của phương trình trên đường tròn lượng giác là: A. . B. . C. . D. . Cho phương trình số giá trị để phương trình có nghiệm là: A. . B. . C. . D. . Phương trình tương đương với phương trình: A. . B. . C. . D. . Phương trình có bào nhiêu nghiệm trên ? A. . B. . C. . D. . Số giá trị nguyên của để phương trình có nghiệm trên là: A. . B. . C. . D. . Phương trình đối xứng và các phương trình lượng giác không mẫu mực. Phương trình có số điểm biểu diễn trên đường tròn lượng giác là: A. . B. . C. . D. . Có bao nhiêu giá trị nguyên của để phương trình có nghiệm? A. . B. . C. . D. . Cho phương trình . Khi đặt thì: A. . B. . C. . D. . Phương trình có nghiệm khi: A. . B. . C. . D. . Cho phương trình . Đặt với thì phương trình tương đương với phương trình: A. . B. . C. . D. . Một số phương trình lượng giác khác. Phương trình có các nghiệm là và . Giá trị của là: A. . B. . C. . D. . Số điểm biểu diễn nghiệm của phương trình trên đường tròn lượng giác là: A. . B. . C. . D. . Phương trình có bao nghiêu nghiệm trên ? A. . B. . C. . D. . Phương trình có bao nhiêu nghiệm trên ? A. . B. . C. . D. . Phương trình có tích các nghiệm trên là: A. . B. . C. . D. . Phương trình có tập nghiệm là: A. . B. . C. . D. . Phương trình có tổng nghiệm âm liên tiếp lớn nhất là: A. . B. . C. . D. . Số nghiệm của phương trình trên là: A. . B. Vô số. C. . D. . Phương trình có bao nhiêu nghiệm trên ? A. . B. . C. . D. . Phương trình có bao nhiêu nghiệm trên ? A. . B. . C. . D. . Phương trình có tập nghiệm là: A. . B. . C. . D. . Phương trình có các nghiệm là: A. . B. . C. . D. . Phương trình có bao nhiêu nghiệm trên ? A. . B. . C. . D. . Phương trình đưa về phương trình tích được phương trình tương đương là: A. . B. . C. . D. . Phương trình là phương trình hệ quả của phương trình: A. . B. . C. . D. . Phương trình có số nghiệm trên là: A. . B. . C. . D. . Phương trình có nghiệm dạng và thì bằng: A. . B. . C. . D. . Phương trình có bao nhiêu nghiệm trên ? A. . B. . C. . D. . Phương trình lượng giác chứa tham số. Phương trình ( là tham số) có nghiệm trên khi: A. . B. . C. . D. . Có bao nhiêu giá trị nguyên âm lớn hơn của để phương trình có hai nghiệm thuộc ? A. . B. . C. . D. . Các giá trị của để phương trình có nghiệm thì: A. . B. . C. . D. . Cho phương trình . Số các giá trị nguyên dương của nhỏ hơn để phương trình có nghiệm là: A. . B. . C. . D. . Phương trình có nghiệm trên khi tất cả các giá trị thỏa mãn: A. . B. . C. . D. . Có bao nhiêu giá trị nguyên của nhỏ hơn để phương trình có nghiệm ? A. . B. . C. . D. . HƯỚNG DẪN GIẢI CHI TIẾT Phương trình lượng giác cơ bản Đáp án B. Mà . Đáp án C. . Biểu diễn trên đường trong lượng giác: Vậy có họ nghiệm thuộc . Đáp án A. Phương trình có nghiệm khi . Đáp án C. Phương trình có nghiệm khi . Đáp án B. Phương trình . Đáp án A. Mà Do nghiệm là , , . Đáp án D. Ta có Đáp án D. Vậy . Đáp án B. (Chú ý gộp nghiệm trên đường tròn lượng giác) Ta có: Mà Vậy có giá trị có nghiệm . Đáp án A. với . Vậy nghiệm âm lớn nhất là . Đáp án D. Vì . Một số phương trình lượng giác thường gặp Đáp án B. Vậy phương trình có nghiệm thuộc là và . Đáp án A. + Với : Phương trình (vô nghiệm) không thỏa mãn. + Với : Phương trình xác định với mọi giá trị . Đáp án C. có nghiệm có nghiệm Vậy có giá trị nguyên thỏa mãn. Đáp án D. Vậy tổng các nghiệm trên là: . Đáp án B. . Vậy . Đáp án A. . Vậy tổng nghiệm dương liên tiếp nhỏ nhất là: . Đáp án C Điều kiện: Phương trình Kết hợp điều kiện suy ra nghiệm của phương trình là Đáp án B. Điều kiện: . Ta có: Phương trình . Đáp án C. Đáp án D. + Với có nghiệm + Phương trình có nghiệm có nghiệm khác . Đáp án B. không có nghiệm thỏa mãn . Phương trình có nghiệm trên . Đáp án D. . Vậy tổng hai nghiệm âm lớn nhất là . Đáp án C. (*) Đặt . Xét trên . Suy ra (*) có nghiệm . Vậy . Đáp án B. Điều kiện . Phương trình Vậy . Đáp án D. Phương trình bậc nhất đối với Đáp án A. Phương trình có nghiệm . Đáp án C. . . Đáp án A. Đáp án C. . Hai nghiệm dương liên tiếp nhỏ nhất là . Đáp án C. Nghiệm dương nhỏ nhất là , nghiệm âm lớn nhất là . Vậy . Phương trình đẳng cấp bậc 2. Đáp án D. Với vô lí. Với chia cả hai vế cho ta được: Vậy số điểm biểu diễn nghiệm trên đường tròn lượng giác là 4. Đáp án C. Phương trình có nghiệm Mà . Vậy có 7 giá trị thỏa mãn. Đáp án B. Phương trình -Với không thỏa mãn phương trình. -Với , chia cả hai vế của phương trình cho ta được Chọn đáp án B. Điều kiện Phương trình . Vây só nghiệm trên là 3. Đáp án C. Trên Đặt Yêu cầu bài toán tìm để phương trình có nghiệm trên Phương trình có nghiệm . Vậy có 3 giá trị nguyên của thỏa mãn. Phương trình đối xứng và các phương trình lượng giác không mẫu mực. Đáp án C. Đặt . + Với + Với . Vậy có 3 điểm biểu diễn các nghiệm. Đáp án D. Đặt . Phương trình có nghiệm trên Xét hàm số trên Phương trình có nghiệm Vậy các giá trị thỏa mãn. Đáp án A. Điều kiện . Phương trình Giải Giải . Đặt , . . Vậy . Chọn đáp án B. Cách 1: Điều kiện để phương tình có nghiệm: Cách 2: Phương trình có nghiệm có nghiệm . Đáp án C. . Đáp án A. . Vậy . Đáp án C. Vậy có 4 điểm biểu diễn nghiệm trên đường tròn lượng giác. Đáp án A. . Vậy phương trình có 1 nghiệm thuộc . Đáp án B. . Vậy phương trình có 24 nghiệm trên . Đáp án B. Suy ra có hai nghiệm thuộc là và . Vậy tích hai nghiệm là . Đáp án A. . Đáp án D. Điều kiện . Ta có . Phương trình . Vậy tổng các nghiệm âm liên tiếp lớn nhất là . Đáp án A. Ta có , mà. Vậy phương tình đã cho vô nghiệm. Đáp án A. Vậy phương trình có 1 nghiệm trên . Đáp án C. Đặt Phương trình Vậy phương trình có 3 nghiệm thuộc . Đáp án B. . Đáp án B. Điều kiện Phương trình . Đáp án B. Điều kiện . Phương trình Vậy phương trình có 4 nghiệm trên Đáp án C. Vậy ta chọn đáp án C. Đáp án D. Vậy ta chọn đáp án D. Đáp án A. Điều kiện: Phương trình - Với : Không thỏa mãn phương trình - Với : Chia hai vế cho ta được: Kết hợp với điều kiện Phương trình vô nghiệm Đáp án A. Điều kiện: Phương trình Đáp án B. Điều kiện: PT: Mà Vậy PT có 33 nghiệm trên Phương trình lượng giác chứa tham số Đáp án C. có nghiệm thuộc Giải PT (1) không có nghiệm nào thuộc (*) có nghiệm có nghiệm . Chú ý: Độc giả có thể giải cách khác như sau: Có Đáp án A. PT có đúng hai nghiệm Giải (1): có hai nghiệm thuộc => Phương trình có hai nghiệm thuộc (2) vô nghiệm hoặc (2) Vậy có 7 giá trị của m thỏa mãn. Chú ý: Đáp án C Đặt , phương trình Bảng biến thiên: => Phương trình (*) có nghiệm . Vậy a + b = -8 Đáp án B Điều kiện: + Từ m = 0 loại do điều kiện phương trình (*) vô nghiệm. + Với => (*) có nghiệm khi (1) Vậy có 9 giá trị của m thỏa mãn. Đáp án B Giải (1): luôn có 2 nghiệm phương trình có nghiệm. Đáp án D Đặt => Yêu cầu bài toán trở thành tìm m để phương trình có nghiệm có nghiệm Bảng biến thiên: => Phương trình có nghiệm Vậy có 2011 giá trị của m nhỏ hơn 2018 + Với thì
Tài liệu đính kèm:
 bai_tap_trac_nghiem_mon_toan_lop_11_co_dap_an_chu_de_1_ham_s.docx
bai_tap_trac_nghiem_mon_toan_lop_11_co_dap_an_chu_de_1_ham_s.docx






